世界最大規模のMatrix計算であるGoogle PageRank は、27億次元の行列(Matrix)の固有値である。このタイトルをもつホームページが、MathWorksのMATRAB(計算ソフト名)のNewsサイトにある。
PageRankとは
何のことやら?と思う人も多いと思うが、情報科学やシステム理論を学ぶひとたちには是非、関心をもっていただきたいと思う。また、ランクupしたいホームページをお持ちの方も、考える価値があるテーマである。サーベイはWikiに掲載:検索の数理
PageRank とは、ホームページの価値の指標であり、グーグル社の商標(PageRank™)でもある。ツールバーを導入して、任意のホームページを開くと、そのページの価値(重要性)が、表示される仕組みになっている。またこれが、キーワード検索のランキングに反映される。

Googleは、特許出願中のPageRankTM 技術 を公開している。長くて読みにくいが、この基本部分は、実にエレガントな固有値計算にある。
出願文書全訳
ページの価値とは
さて、サーチエンジンがどのようにページを重要度に応じて表示するか、考えたい。
文章での説明
Webの膨大なリンク構造を用いて、その特性を生かします。ページAからページBへのリンクをページAによるページBへの支持投票とみなし、Googleはこの投票数によりそのページの重要性を判断します。しかしGoogleは単に票数、つまりリンク数を見るだけではなく、票を投じたページについても分析します。「重要度」の高い ページによって投じられた票はより高く評価されてそれを受け取ったページを「重要なもの」にしていくのです。こうした分析によって高評価を得た重要なページには高いPageRankTM (ページ順位)が与えられ、検索結果内の順位も高くなります。
グラフによる説明
1.行列 A:ページ i から別のページ j へリンクが張られている場合にはその成分を 1 とし、そうでない場合を 0 とする。これを 隣接行列と呼ぶ。
行列 A の成分 aij は、
aij = 1 if (ページ i からページ j へのリンクが「ある」場合)
0 if (ページ i からページ j へのリンクが「ない」場合)
2.次に、行列 A の列和が1となるように各列を修正する。(被リンク数のスコア合計=1)
3. その行列の転地行列をつくる。これを 行列 S:状態推移確率行列と呼ぶ。(転置する理由は、PageRank が「どれだけリンクしているか」ではなく「どれだけリンクされているか」を重視するため)
4.基本行列の最大固有値とそれに対応した固有ベクトルを求める。 各ページの重要度:固有ベクトルの値
(注)N次正方行列 S に対して Sx = λx を満たす数λをAの固有値といい、x をλに属する固有ベクトルという
AからEの5ページの引用(リンク)されている場合で説明する。
(参考)
A,B,C,D,Eに、それぞれ重要度(x1,X2,X3,X4,X5)という未知の重要度があり、Aは3つのページB、C、Dから参照されている図であるから、Aの重要度X1は X1=1/3*X2+1/3*x3+1/3*X4 と考えるのである。
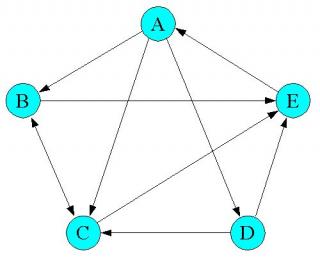
この場合の隣接行列は、定義より

これを列合計を1として正規化した行列 M は、下記のとおり。
M=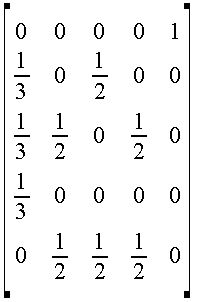
これを、数式で示せば、X*M = X となる。Mは上記行列。Xは(x1,X2,X3,X4,X4)の行ベクトル。
この 固有値問題の解の、PageRankは 下記のようになる。
(x1,X2,X3,X4,X4)=(1/4,7/36,2/9,1/12,1/4)
ページのランキング順位は、A.E,C,B,D の順となる。(但し、A=E)
この固有値問題の数値計算方法は、いろいろ考えられる。
1.最も素朴な方法は、適当な値最初はすべてのxi=1 として 初期値x0ベクトルを用いて、X1=S*x0 次にX2=S*x1 X3=S*x2と繰り返し、収束するまで何回も繰り返して 答えを求める方法。Sは状態推移確率行列(行合計が1の行列)です。
2.もうひとつは、最大固有値を求める問題は、下記の最適化問題と同じ という性質を使う方法
xt S x —> 最大化
制約:xは長さ1の正規ベクトル (Σ(xi)2 = 1)
これも、前のPageRankを初期値として繰り返し法で解けるが、安定解(最適値)を求めるのに時間がかかる。Googleのランキングが変動する(ひとによってはグーグルダンスと呼ぶ)が、このあたりに原因があるのかも・・・。
いずれにせよ、巨大Matrixの固有値問題を厳密に解くには時間がかかる。 よくぞ 部分分解して小規模化するにしても 解く気になったのが 素晴らしい 。
これを世界中のWebPage で求めるには、ものすごく力強いcomputationが必要でしょう。
高速の解法なども、サーベイ論文で紹介されている。あとは、勉強してください。
Googleの若き経営者であり、創業者にSergey Brin と Larry Pageがいる。彼らが1998年スタンフォード大学の学生の頃、PageRankの計算アルゴリズムの研究を行い、研究発表と併せてgoogleの創業に勤めている。 Sergey Brinの研究論文も、有名なようだ。
当時、といっても7年しか経っていないが、このような検索アルゴリズムが特許になり、なおかつ Googleが時価総額7兆円に迫る巨大企業になるとは、誰もわからなかったのだろう。
さて、ここで、検索のランクを上げる方法について、原理に沿って考えたい。
1.被リンク数 (単純な意味での人気度) が多いこと
2.評価の高いページからのリンクが多いこと (裏付けのある人気)
3.リンク元ページでの他リンク数が少ないこと (選び抜かれた人気)
以上の3つしかない。良く検索エンジンに登録するとupするとか、検索される数が多いほど良いとか言われるが 全く 根拠がないことになるし、あなたのホームページの視聴率をupするビジネスもあるが、あまり信用しないほうが良い。また、よく検索のキーワードも関係ない。
GoogleのPageRankは、極めて合理的である。
評価の高い(たくさん参照される)サイトに厳選されて参照されることだけである。
順序付けや重み付けの研究は、古くから、計量心理学や経済学の分野でもあった。また、意思決定や社会選択の理論も古くから発達してきた。
最近使われる、AHP(Analytic Hierarcy Process)など、解り易い(これも項目に重み付けを行う固有値解法)ので、乱用される状況である。また、心理学の多次元尺度構成や一対比較法もその傾向がある。重要なのは、システム構造に注目し、リアリティのある評価ができることである。
例えば、Webページの価値は、人間の身長のように、平均の周りで一定の分散をもったようなものと考えるならば、心理学の方法もありうるが、そうではない。また、参照されることと参照していることに価値の違いがないとすれば、対照性を仮定している一対比較やAHPも使えるだろうが、WEBの世界は異なっている。ある状態(ページ)からある状態(ページ)に推移(参照)しながら、閲覧する世界、また検索しながら閲覧する世界では、Googleの方法は、下記の点で合理的である。
1.ページの価値を事前に与えず、リンク状況の変化に合わせて評価を変える(成長の原理)を取り込んでいること
2.ページの価値は、スケールフリーと見ていること
3.参照する、されるを同等としない非対称性を導入(納得性)
4.このことで、人為的にランクを上げる手段を抑止していること
1998年当時、PageRankと異なるもひとつのプロジェクトHitsがあった。その手法と比べても、PageRankの合理性が示される論文がある。
(参照:Markov Cluster Algorithm を用いたWeb コミュニティ群の発見手法:Hits批判 )
ここで、問題設定。
1.もし、Google検索がドミナントとなり、皆がこの順位での高いページを見て、参照するようになれば、世界のページのリンク構造は、PageRankの成長原理に沿って動くことになる。その場合、スケールフリーのべき乗則は維持されるだろうか。
「あるノードがk個のリンク数を持つ確率は1/kn(nは約2)に比例しており、その分布は「べき乗則」とよばれる」
2.もうひとつ
やはり、閲覧数*閲覧時間の合計が、ページの価値に対応しているようにも思えるが、これを,
あるいはこの代理指標を測定し、PageRankとする評価方法はあるか。
なお、PageRankは、より高度に、より精緻になっているようだ。
参考:http://www.sem-r.com/sem/seo/
:最近の 自宅 サーバー 構築方法:Wiki Blog(ブログ) CMS を使う
2004年に発表されたdeeper inside pagerankという英文論文と公表されたグーグルのpagerank特許内容からみて、固有値は、明らかに、関係ありません。(相当以前は、確かに固有値問題と考えられていたようです。)それにしても日本では、何故こんな簡単なことが誤解されなければならないのでしょうか?と思います。http://www.geocities.jp/existenzueda/pagerank_theory.htmご参照。
このページ(http://www.geocities.jp/existenzueda/8.ht)にてリンクした英文のウェブサイト・論文や特許内容を読むだけで一目瞭然ではないでしょうか。?ご感想があれば、ご記入頂ければ幸いです。楽しみにしております。
2004年に発表されたdeeper inside pagerankという英文論文と公表されたグーグルのpagerank特許内容からみて、固有値は、明らかに、関係ありません。(相当以前は、確かに固有値問題と考えられていたようです。)それにしても日本では、何故こんな簡単なことが誤解されなければならないのでしょうか?と思います。http://www.geocities.jp/existenzueda/pagerank_theory.htmご参照。
このページ(http://www.geocities.jp/existenzueda/8.ht)にてリンクした英文のウェブサイト・論文や特許内容を読むだけで一目瞭然ではないでしょうか。?ご感想があれば、ご記入頂ければ幸いです。楽しみにしております。
サーベイ論文にて、deeper inside pagerankにリンクされていますが、読まれたのでしょうか?。http://www.geocities.jp/existenzueda/8.htm
にて、2番目に大きい固有値は、1-α(0.85)である旨証明されています。
私は、次のように書きましたが、誤った点があれば、教えていただけませんか?。
http://www.geocities.jp/existenzueda/mathemat.htmより
(初等数学をご存知の方用)
ページランクの算出が、上記のような手法で、算出されていることは、特許文書に示されている、下記の式から明白です。
p∞=limAnp0 (n→∞) なお、例えば、p2 =Ap1=A2p0である旨、特許文書に明記されています。
p0が、初期ベクトル(この例では、1,0,0)。Aは、英語でグーグル行列と呼ばれる下記の行列です。(行列としては、Stochastic transition matrix、日本語では、確率推移行列に属します。)
A=(α/N ×1 )+(1-α)B この行列の詳細は、現実のページランク算出方法を見てください。1 は、太字にしていますが、ベクトルではなく、行列です。
サーベイ論文にて、deeper inside pagerankにリンクされていますが、読まれたのでしょうか?。http://www.geocities.jp/existenzueda/8.htm
にて、2番目に大きい固有値は、1-α(0.85)である旨証明されています。
私は、次のように書きましたが、誤った点があれば、教えていただけませんか?。
http://www.geocities.jp/existenzueda/mathemat.htmより
(初等数学をご存知の方用)
ページランクの算出が、上記のような手法で、算出されていることは、特許文書に示されている、下記の式から明白です。
p∞=limAnp0 (n→∞) なお、例えば、p2 =Ap1=A2p0である旨、特許文書に明記されています。
p0が、初期ベクトル(この例では、1,0,0)。Aは、英語でグーグル行列と呼ばれる下記の行列です。(行列としては、Stochastic transition matrix、日本語では、確率推移行列に属します。)
A=(α/N ×1 )+(1-α)B この行列の詳細は、現実のページランク算出方法を見てください。1 は、太字にしていますが、ベクトルではなく、行列です。
LangvilleさんとMeyerさんの論文”deeper inside pagerank"にありますよに、ページランク問題の解法とは、「マルコフ連鎖行列の定常解を求めること」です。これは、論文にありますようにΠtP=πtなる性質を満たす固有値問題(eigenvaue problem)の解をもとめることと同等です。
行列が、縮退したりしないなどのadjustmentを2度行うのでPを若干修正していますが、本質は変わりません。著者もajustmentと呼んでいます。
最も素朴な定常解の求め方は、ご存知のとおり初期ベクトルπを適当に置いて収束するまでPと掛けて繰り返すことです。でもこの方法は実用に耐えないので、いろいろな工夫がありますが、そのあたりは論文や特許をご覧ください。
LangvilleさんとMeyerさんの論文”deeper inside pagerank"にありますよに、ページランク問題の解法とは、「マルコフ連鎖行列の定常解を求めること」です。これは、論文にありますようにΠtP=πtなる性質を満たす固有値問題(eigenvaue problem)の解をもとめることと同等です。
行列が、縮退したりしないなどのadjustmentを2度行うのでPを若干修正していますが、本質は変わりません。著者もajustmentと呼んでいます。
最も素朴な定常解の求め方は、ご存知のとおり初期ベクトルπを適当に置いて収束するまでPと掛けて繰り返すことです。でもこの方法は実用に耐えないので、いろいろな工夫がありますが、そのあたりは論文や特許をご覧ください。
ありがとうございます。
Google創設者の論文(The Pagerank Citation Ranking)の図5を印刷され注意深く、ご覧頂ければ、反復計算を最後まで完了していないことが、お分かりいただけると思うのですが?(本文では、執筆者は、計算対象のウェブページ数の増加が、反復計算回数にほとんど影響しないことを強調していますが・・。)
そこで、「実用に耐えない」とは、計算が、最後まで終わらないというご趣旨なのでしょうか?教えて頂けないでしょうか。?
また、公開されているページランク特許と上記の論文は、既に丹念に読んだつもりですが、ページランク特許からみると、初期値を1/N(Nは、計算対象のウェブページ数)とする単純なパワー法で算出しているとしか、思えないのですが。?あわせて教えていただければ、幸いです。
(私の勝手な推測ではなく、名大助教授の学会報告でも、同様の見解が、報告されております。http://www.geocities.jp/existenzueda/pagerank_theory.htmご参照)
また、http://www.geocities.jp/existenzueda/pagerank_theory.htmを流し読み頂き、誤りがあれば、ご指摘頂ければ、本当に助かります。私の趣味とは言え、誤ったことを書いていれば、訂正したいと思います。)
長くなり、すみません。楽しみにしております。
ありがとうございます。
Google創設者の論文(The Pagerank Citation Ranking)の図5を印刷され注意深く、ご覧頂ければ、反復計算を最後まで完了していないことが、お分かりいただけると思うのですが?(本文では、執筆者は、計算対象のウェブページ数の増加が、反復計算回数にほとんど影響しないことを強調していますが・・。)
そこで、「実用に耐えない」とは、計算が、最後まで終わらないというご趣旨なのでしょうか?教えて頂けないでしょうか。?
また、公開されているページランク特許と上記の論文は、既に丹念に読んだつもりですが、ページランク特許からみると、初期値を1/N(Nは、計算対象のウェブページ数)とする単純なパワー法で算出しているとしか、思えないのですが。?あわせて教えていただければ、幸いです。
(私の勝手な推測ではなく、名大助教授の学会報告でも、同様の見解が、報告されております。http://www.geocities.jp/existenzueda/pagerank_theory.htmご参照)
また、http://www.geocities.jp/existenzueda/pagerank_theory.htmを流し読み頂き、誤りがあれば、ご指摘頂ければ、本当に助かります。私の趣味とは言え、誤ったことを書いていれば、訂正したいと思います。)
長くなり、すみません。楽しみにしております。
言葉足らずでしたようですので、補足します。
ページランク算出は、Google創設者の論文(The Pagerank Citation Ranking)とウェブ上でその後公開された特許内容からて、
①ページランク算出上、Google行列の主固有ベクトルの完全な値(安定解)を求める必要は、実用上は、全くないとページランク考案者は、考えた。(特許文書では、10回の反復でも意味のある数値を得られれるとしています。また、論文では、上記のとおりです。)
②ページランク考案者は、実用的には、近似値で十分であると考えた。
と思われます。
この点については、真の意味で、この分野の専門研究者の方(例:上記の名大助教授、計算理工学専攻)ですら、気づいておられないようなのです。
この点が、学者の方と、起業家の決定的な相違であるように思われるのです。
即ち、明確に言えば、記入頂いた「実用に耐えないので・・・」云々の部分のご趣旨が、私には、理解困難なのです。気にされられるかもしれませんが、全く逆のように思われるのですが・・・・?。
言葉足らずでしたようですので、補足します。
ページランク算出は、Google創設者の論文(The Pagerank Citation Ranking)とウェブ上でその後公開された特許内容からて、
①ページランク算出上、Google行列の主固有ベクトルの完全な値(安定解)を求める必要は、実用上は、全くないとページランク考案者は、考えた。(特許文書では、10回の反復でも意味のある数値を得られれるとしています。また、論文では、上記のとおりです。)
②ページランク考案者は、実用的には、近似値で十分であると考えた。
と思われます。
この点については、真の意味で、この分野の専門研究者の方(例:上記の名大助教授、計算理工学専攻)ですら、気づいておられないようなのです。
この点が、学者の方と、起業家の決定的な相違であるように思われるのです。
即ち、明確に言えば、記入頂いた「実用に耐えないので・・・」云々の部分のご趣旨が、私には、理解困難なのです。気にされられるかもしれませんが、全く逆のように思われるのですが・・・・?。
大規模な行列の固有値を反復計算法(単純なパワー法)で近似計算した場合
収束のスピードは、P行列と初期値によって収束のスピードが大きく変わります。ホームページの連結状況によってP行列の値が、日々異なってくるので、近似計算にならざるを得ないでしょうが、安易に少数の回数で打ち切ると、ご存知のように、毎月のGoogleダンスといわれた大幅なpagerankの変動となって、ユーザーは、驚いてしまうでしょう。
最近は、googleダンスも昔のように、酷くないので、初期値や収束アルゴリズムに改良が加えられているようです。(条件次第では、ランキングが不安定になり易いので)
ユーザーが直感的に耐えられる範囲の近似計算で、高速なものが実用に耐えられる方法でしょう。多数のバリエーションがあるでしょう。
1.初期値
2.P行列のadjustmentや分割方法
3.繰り返し収束アルゴリズム
などの工夫です。。
固有値の計算法がどんどん進化したように、特殊なP行列の解法(状態推移確率行列の数値解法)もどんどん進化していくでしょう。
大規模な行列の固有値を反復計算法(単純なパワー法)で近似計算した場合
収束のスピードは、P行列と初期値によって収束のスピードが大きく変わります。ホームページの連結状況によってP行列の値が、日々異なってくるので、近似計算にならざるを得ないでしょうが、安易に少数の回数で打ち切ると、ご存知のように、毎月のGoogleダンスといわれた大幅なpagerankの変動となって、ユーザーは、驚いてしまうでしょう。
最近は、googleダンスも昔のように、酷くないので、初期値や収束アルゴリズムに改良が加えられているようです。(条件次第では、ランキングが不安定になり易いので)
ユーザーが直感的に耐えられる範囲の近似計算で、高速なものが実用に耐えられる方法でしょう。多数のバリエーションがあるでしょう。
1.初期値
2.P行列のadjustmentや分割方法
3.繰り返し収束アルゴリズム
などの工夫です。。
固有値の計算法がどんどん進化したように、特殊なP行列の解法(状態推移確率行列の数値解法)もどんどん進化していくでしょう。
ありがとうございました。
宇宙物理学専攻のある方のページランクに関するウェブページを批判している私の上記のウェブページの内容に誤りはなかったと言うことですね。
ところで、グーグルダンスについてですが、2003年の夏頃まで、検索結果の表示順位が、毎月変わるのでそう呼ばれておりましたが、現在は、完全に解消されております。(直接的には、PRと無関係の他の要因による表示順位の変動であったと思います。)
Matt Cutts 氏(同氏は、間違いなく、グーグル内部の方です)の下記のブログを是非お読み下さい。http://www.mattcutts.com/blog/explaining-algorithm-updates-and-data-refreshes/
(原文を読まれた場合、上記ブログにあるWMWは、分かりにくいでしょうが、web master world の略で、アメリカで最も一般的なSEO関係のフォーラムです。)
また、同氏のブログの重要部分の趣旨をまとめたページをこしらえていますので、良ければ見ていただいて感想などご記入下さい。
http://www.geocities.jp/existenzueda/6.htm
ありがとうございました。
宇宙物理学専攻のある方のページランクに関するウェブページを批判している私の上記のウェブページの内容に誤りはなかったと言うことですね。
ところで、グーグルダンスについてですが、2003年の夏頃まで、検索結果の表示順位が、毎月変わるのでそう呼ばれておりましたが、現在は、完全に解消されております。(直接的には、PRと無関係の他の要因による表示順位の変動であったと思います。)
Matt Cutts 氏(同氏は、間違いなく、グーグル内部の方です)の下記のブログを是非お読み下さい。http://www.mattcutts.com/blog/explaining-algorithm-updates-and-data-refreshes/
(原文を読まれた場合、上記ブログにあるWMWは、分かりにくいでしょうが、web master world の略で、アメリカで最も一般的なSEO関係のフォーラムです。)
また、同氏のブログの重要部分の趣旨をまとめたページをこしらえていますので、良ければ見ていただいて感想などご記入下さい。
http://www.geocities.jp/existenzueda/6.htm
「グーグルページランクと検索結果表示順位について」という、丁寧な解説がありました。ご参考まで。
http://www.geocities.jp/existenzueda/
「グーグルページランクと検索結果表示順位について」という、丁寧な解説がありました。ご参考まで。
http://www.geocities.jp/existenzueda/